Methoden

FLAPW

Eine genaue und realistische Bescheibung von Materialien von wissenschaftlichem oder technologischem Interesse erfordert ab-initio Methoden die eine Reihe von Phänomenen wie nicht-kollinearen Magnetismus, Spin-Bahn-Wechselwirkungseffekte, (externe) elektrischen Felder, Korrelationseffekte, niedrige Dimensionen, etc. behandeln können. Wir haben im Rahmen der Vektor-Spindichtefunktionaltheorie ein Programm entwickelt, FLEUR, das uns erlaubt Materialeigenschaften auf einem quantenmechanischem Niveau zu untersuchen. Dieses massiv parallelisierte Programm beruht auf der full-potential-linearized-augmented- planewave-(FLAPW)-Methode für Volumens-, Oberflächen- und Kettengeometrie. Mit dieser Methode ist es möglich, eine große Vielfalt von Systemen mit offenen Strukturen und niedirger Symmetrie zu untersuchen. Die Berechnung der Kräfte erlaubt es gleichzeitig den magnetischen wie auch den strukturellen Grundzustand zu bestimmen.

mehr

(S. Blügel)

Orbitalabhängige Dichtefunktionale

Viele Jahre lang kamen lokale und semilokale Funktionale, wie die Lokale-Dichte-Näherung und die Verallgemeinerte Gradientennäherung, standardmäßig in Dichtefunktionalrechnungen der Elektronenstruktur zum Einsatz. Mit dem enormen Anstieg der Computerrechenleistungen ist es heute möglich, fortgeschrittene nicht-lokale orbitalabhängige Funktionale auf komplexe Systeme anzuwenden. Hybridfunktionale sind die einfachsten Funktionale dieser Art. Sie enthalten das exakte Austauschfunktional, so dass der Selbstwechselwirkungsfehler teilweise aufgehoben wird, was die Beschreibung von stark korrelierten Systemen und Oxiden verbessert. Wir haben zwei der bekanntesten Funktionale (PBE0 und HSE) in den FLEUR-Code implementiert. Orbitalabhängige Funktionale können auch im Rahmen der Kohn-Sham-Formulierung behandelt werden. Hierzu verwendet man die Methode des optimierten Effektivpotentials (OEP). Mit einer numerischen Korrektur hinsichtlich der Basissatzunvollständigkeit konnte die Methode entscheidend verbessert werden. Als nächster logischer Schritt planen wir die Hinzunahme eines nicht-lokalen und frequenzabhängigen Korrelationsfunktional, das in der Lage ist, Van-der-Waals-Kräfte aus ersten quantenmechanischen Prinzipien zu beschreiben. Mit dem Fluktuations-Dissipations-Theorem in adiabatischer Verbindung ist es weiterhin möglich, aus der Dichte-Dichte-Korrelationsfunktion systematisch neue Dichtefunktionale herzuleiten, wodurch eine Verbindung mit der Vielteilchenstörungstheorie hergestellt wird.

(M. Betzinger, M.Schlipf, C. Friedrich )

Exakte Diagonalisierung

Eine nahe liegende Methode das Vielteilchenproblem zu lösen ist es, einfach den Hamilton-Operator zu diagonalisieren. Natürlich ist das nur für Systeme endlicher Größe und mit endlich vielen Freiheitsgraden möglich. Dann ist nämlich der Hamilton-Operator eine Matrix mit endlicher Dimension. Allerdings wächst diese Dimension mit zunehmender Systemgröße schnell auf astronomische Größen an. Schon für recht kleine Cluster benötigt man bis zu 10 Gigabyte Speicherplatz, allein um eine einzige Vielteilchen-Wellenfunktion zu speichern. Deshalb ist es, obwohl man das Vielteilchen-Problem exakt löst, sehr schwierig, Korrelationseffekte von den Auswirkungen der Kleinheit des Systems zu unterscheiden. In unseren Arbeiten nutzen wir die Lanczos-Methode zur Berechnung des Grundzustandes, der Dichtematrix, der Spektralfunktion und von dynamischen Antwortfunktionen.

(E. Koch)

Quanten-Monte-Carlo

Für große Systeme wird der Hilbert-Raum extrem groß. Dann ist es nicht einmal mehr möglich, etwa das Produkt der Hamilton-Matrix mit einem Zustandsvektor exakt zu berechnen. Die Grundidee des Quanten-Monte-Carlo-Verfahrens besteht nun darin, solche Matrix-Vektor-Produkte stochastisch auszuwerten. Sind alle Matrixelemente des Hamilton-Operators positiv, so erlaubt diese Methode die, bis auf kontrollierbare statistische Fehler, exakte Bestimmung des Grundzustandes sehr großer Vielteilchen-Systeme. Betrachtet man jedoch wechselwirkende Elektronen, so folgt aus dem Pauli-Prinzip, dass es immer auch negative Matrixelemente gibt. Diese sind für das gefürchtete Vorzeichenproblem in der Quanten-Monte-Carlo-Simuation verantwortlich. Wir verwenden die sog. fixed-node-Näherung, um dem Vorzeichenproblem zu entgehen. Mittels QMC-Rechungen bestimmen wir Grundzustände, statischen Antwortfunktionen und Quasiteilchen-Energien.

(E. Koch)

Die KKR Methode

Die KKR Methode für die Berechnung der Bandstruktur von Festkörpern wurde 1947 von Korringa und 1954 von Kohn und Rostoker eingeführt. Die Methode basiert auf der Vielfachstreuungtheorie für die Lösung der Schrödingergleichung. So wird das Problem in zwei Schritten gelöst. Zuerst wird das Streuproblem eines einzelnen Potentials im freien Raum gelöst; danach wird das Problem der Vielfachstreuung von allen Atompotentialen gelöst, unter dem Ansatz, dass die einfallende Welle auf jedem Potential die Summe der gestreuten Wellen aller anderen Potentialen ist.

Die KKR Methode hat sich sehr erfolgreich als Greensche Funktionsmethode im Rahmen der Dichtefunktionaltheorie erwiesen. Ihre Anwendungen umfassen ab-initio Rechnungen vom Bulk von Festkörpern, von Oberflächen, Grenzflächen, und Schichtsystemen mit O(N) Skalierung, sowie auch die Einbettung von Defekten und Clustern im Bulk und auf Oberflächen. Die Methode ist erfolgreich angewendet worden auf nichtkollinearen magnetischen Strukturen, Gitterrelaxationen, relativistischen Effekten, und der Transporttheorie in Festkörpern.

“Minimum Search Nudged elastic band” Optimierer (MsNEB)

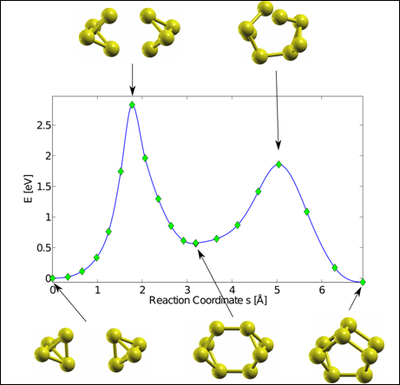
Optimierung ist essenziell in vielen wissenschaftlichen und ökonomischen Bereichen. Solche Optimierungsprobleme sind aber meist zu komplex um mit direkten Rechnungen oder mit „Trial and Error“ gelöst zu werden. Zwei bekannte Methoden, die tiefliegende Minima in komplexen Systemen finden können, sind die „Simulated Annealing“ Methode und der „Genetische Algoritmus“. In diesen Methoden kontrollieren künstliche Fluktuationen die Wahrscheinlichkeit einem lokalen Minimum einer gewissen tiefe zu entkommen. Hier wird eine komplementäre Methode entwickelt, die auf der „Nudged Elastic Band“ Methode, die üblicherweise zur Bestimmung von Sattelpunkten verwendet wird, basiert. Hierbei hängt die Wahrscheinlichkeit einem lokalen Minimum zu entkommen von dessen Ausdehnung nicht von dessen Tiefe ab.

Diese junge Methode hat bereits ihr Können unter Beweis gestellt, indem sie, im Rahmen der Dichtefunktionaltheorie (DFT), die stabilsten Isomere der Phosphor P₄, P₈  Moleküle, sowie der entsprechenden Moleküle von As_n, Sb_n, und  Bi_n (n = 4,8) gefunden hat. Im Fall n = 8 fand die Methode stabile und metastabile Konfigurationen, von denen manche neu waren und ähnliche Energie besitzen. Als Nebenprodukt wird eine obere Grenze für die Energiebarriere zwischen diesen Konfigurationen erhalten.

( J.Hischfeld, H.Lustfeld)